𝟑 — Математическая жирная цифра три: U+1D7D1
Значение символа
Математическая жирная цифра три. Математические буквы и цифры.
Символ «Математическая жирная цифра три» был утвержден как часть Юникода версии 3.1 в 2001 г.
Свойства
| Версия | 3.1 |
| Блок | Математические буквы и цифры |
| Тип парной зеркальной скобки (bidi) | Нет |
| Композиционное исключение | Нет |
| Изменение регистра | 1D7D1 |
| Простое изменение регистра | 1D7D1 |
Похожие символы
Кодировка
| Кодировка | hex | dec (bytes) | dec | binary |
|---|---|---|---|---|
| UTF-8 | F0 9D 9F 91 | 240 157 159 145 | 4036861841 | 11110000 10011101 10011111 10010001 |
| UTF-16BE | D8 35 DF D1 | 216 53 223 209 | 3627409361 | 11011000 00110101 11011111 11010001 |
| UTF-16LE | 35 D8 D1 DF | 53 216 209 223 | 903401951 | 00110101 11011000 11010001 11011111 |
| UTF-32BE | 00 01 D7 D1 | 0 1 215 209 | 120785 | 00000000 00000001 11010111 11010001 |
| UTF-32LE | D1 D7 01 00 | 209 215 1 0 | 3520528640 | 11010001 11010111 00000001 00000000 |
Загадки про цифру 3 (три) для детей с ответами
Один плюс два,
Как не крути,
Всегда получишь
Только … (три).
Учим букву,
Учим цифру.
Что за чудо! Посмотри!
Букву «З, з»
Мы видим точно,
А читаем цифру… (три).
Светофор мне улыбнулся
И моргнул глазком своим.
Знают все цвета такие,
Их мы видим ровно … (три).
За одним идёт ведь двойка.
Знают все ученики.
А за двойкой следом тройка,
А, вернее, цифра … (три).
Сколько месяцев в каждом времени года? (три)
Что за чудо,
Что за цифра!
Знает каждый сорванец.
Даже в нашем алфавите
У неё сестра – близнец. (три)
Вот пришла зима к нам в гости,
Погостила и ушла.
А за ней весна примчалась,
Долго тоже не была.
Лето красное настало,
Отзвенело, отцвело.
Осень мигом прилетела,
В школу я уже пошёл.
Цифры я учу и знаю:
Сколько месяцев в году.
Сколько их в зиме и в лете,
И в весне, и в осени.
Вы спросите – я скажу! (три)
Любимая цифра в сказках: «… медведя», «… поросёнка», «… богатыря». (три)
Цифра эта без очков,
Состоит из двух крючков. (три)
Красный, жёлтый и зелёный –
… огня на светофоре. (три)
Ты, попробуй, угадай – ка!
Эта цифра ведь зазнайка.
Один сложишь если с двойкой,
То получишь цифру … (тройку).
У моего сына есть брат, у его брата тоже есть брат. Сколько у нас в семье человек? (три: родитель, два сына)
В небе ласточка, смотри!
Словно наша цифра … (три).
Если видишь красный свет,
Говори: «Проезда нет!»
Если жёлтый свет горит,
Умный вовсе не спешит.
Я зелёный свет люблю,
На него быстрей иду.
Сколько всех цветов? Скажи.
Ты подумай, не спеши. (три)
Сколько желаний исполняет золотая рыбка? (три)
Джина ты поймать спеши,
Он поможет от души.
Слишком много не проси,
Он исполнит только … (три).
Взял кольцо весельчак,
Рубанул быстро так.
Полкольца плюс полкольца
И спаял он два конца.
Удивись и посмотри,
Получилась цифра … (три).
Дополните окончания предложений. Но будьте внимательны!
«В гостях у цифровых сказок»
В лесу в избушку загляни,
Медведя в ней живёт аж …(три).
Другую сказку посети,
И Белоснежку в ней спаси,
А гномиков там целых …(семь).
Щуку в проруби слови
И немножко потряси.
Она желанья исполняет,
Не знаю точно, может …(три).
На море срочно полети,
Морскую пену разверни.
На побережье выйдут тут же
Заморские богатыри.
Их будет точно… (тридцать три).
Цветик – семицветик на лугу сорви.
Желаний много не бывает,
Но он исполнит только …(семь).
Волк стучится в домик чей – то.
Кто живёт там, посмотри.
Пятачок в окошко видно,
Не один, а целых …(три).
Другие загадки:
Картинка 3 — три
Несколько интересных детских загадок
- Загадки про цифру 1 — Один для детей с ответами
Я на клюшку так похожа,
И по виду кочерга.
Со мною надо быть по строже.
Угадай скорей. Кто я? единица - Загадки про Ящерицу для детей с ответами
Малюсенькая,
Лёгонькая,
А за хвост поднять не сможешь!
(Ящерица). - Загадки про Солнце, солнышко для детей с ответами
Что за блинчик жаркий, жёлтый?
Он висит над головой.
Свои лучики-иголки
Посылает за тобой.
Загорать под ним приятно,
Когда лето и тепло.
А зимой искрится ярко
На снегу оно порой! (Солнышко) - Загадки про Картошку, картофель для детей с ответами
Этот овощ самый главный,
Этот овощ-генерал,
Если вы его сварили,
Не забудьте мундир снять.
Ответ: картофель - Загадки про цифру 6 — Шесть для детей с ответами
Если мы возьмем пятерку,
Дорисуем ей овал,
То получим мы (шестерку)
Число 3 | Математика, которая мне нравится
Пишите об интересных свойствах числа
. Картинки приветствуются!
Картинки приветствуются!
Для начала выкладываю свойства числа три, которые прислал Лейб Александрович Штейнгарц.
1. Число 3 – наименьшее нечетное простое число.
2. Магический, или волшебный квадрат — это квадратная таблица , заполненная числами таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова.
Наименьшим магическим квадратом является квадрат ТРЕТЬЕГО порядка. При этом постоянная сумма этого квадрата (равная 15) делится на 3.
3. Через любые три точки, не лежащие на одной прямой, проходит одна и только одна плоскость.
Поэтому стол с четырьмя ножками часто шатается, а с тремя шататься не может. И по этой же причине подставка для фотоаппарата делается с тремя ножками.
4. Сравнительно недавно, только в 16 веке, Николай Коперник понял, что наша Земля – это ТРЕТЬЯ планета, считая от Солнца.
Вокруг Солнца движутся восемь планет в следующем порядке:
Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун.
5. Русская тройка — старинная русская запряжка лошадей. Тройка была придумана для быстрой езды на длинные расстояния.
6. Слово “ТРИ” состоит из ТРЕХ букв.
7. В записи цифры 3 выделяются ТРИ особые точки:
8. Для облегчения выполнения электропроводки, кабели проводов изготавливаются трехцветными. Монтаж сети предполагает применение кабеля с тремя проводами, обозначающими заземление, ноль и фазу. Для облегчения выполнения электропроводки, кабели проводов изготавливаются трехцветными. Монтаж сети предполагает применение кабеля с тремя проводами, обозначающими заземление, ноль и фазу.
9. Вальс (фр. valse) – общее название бальных и народных танцев музыкального размера
. Наиболее распространена фигура в вальсе – несколько полных оборотов с ТРЕМЯ шагами в каждом.
10. Многоугольник с ТРЕМЯ сторонами, то есть треугольник, обладает замечательным свойством – это жесткая фигура. Это означает, что при постоянной длине сторон нельзя изменить форму треугольника. Это свойство треугольника делает его незаменимым в технике и строительстве.
Элементы конструкции в форме треугольника сохраняют свою форму, в отличие, например, от элементов в форме квадрата или параллелограмма.
11. Трёхмерное пространство – геометрическая модель материального мира, в котором мы находимся. Это пространство называется трёхмерным, так как оно имеет три измерения – высоту, ширину
и длину.
12. ТРИ — это единственное слово, которое является одновременно и числительным, и глаголом.
13. На циферблате часов часто изображают только числа, которые делятся на ТРИ.
14. Трезубец – в греческой мифологии оружие морского бога Посейдона. Трезубец состоит из длинного древка и наконечника, увенчанного тремя зубцами.
15. Наименьшее количество фигур, которое может остаться по окончании шахматной партии, это – ТРИ.
16. Многоточие – знак препинания в виде ТРЁХ поставленных рядом точек. В большинстве случаев обозначает незаконченную мысль или паузу автора. В просторечии многоточие также иногда называют “троеточием”.
В математике многоточие используется в значении “и так далее” и, в частности, означает пропуск части последовательности, суммы, произведения и т. п.
Например:
— это сумма чисел от
до
.
— это последовательность натуральных чисел.
Цифра 3 в картинках, загадках и пословицах
Изучать цифру 3 можно разными способами. Помочь в этом могут многочисленные творческие задания и фольклор: пословицы, поговорки, загадки, стихи на русском языке, а также раскраски и картинки. Если вы готовите занятие в 1 класс, вам поможет яркая презентация, которую можно скачать на сайте.
Если вы готовите занятие в 1 класс, вам поможет яркая презентация, которую можно скачать на сайте.
Здесь можно посмотреть и скачать презентацию про число и цифру 3.
На что похожа цифра 3?
Помочь дошкольнику или ребенку, который ходит в 1 класс, запомнить цифру 3, может вопрос: на что она похожа? Чтобы ответить на него, дайте малышу подсказки в виде загадки, цифр в картинках. В фольклорных жанрах часто проводятся ассоциации между цифрами и предметами, явлениями. Например, тройка похожа на крючок, на половину восьмерки и т.д. Если малыш все же не может провести параллель, помогите ему, показав фото различных предметов.
Дать возможность освоить цифры не только дошкольникам, но и ребятам, посещающим 1 класс, может раскраска. Она не только учит цветам и цифрам, но и вырабатывает усидчивость и внимание. Раскраска также поможет малышу ответить, на что похожа цифра 3. Раскраска, распечатанная с нашего сайта, может стать дополнением к уроку или быть использована как задание для минутки отдыха. Раскраска может иметь множество функций. Если вы сомневаетесь, что задать на дом дошкольнику после урока, вам поможет раскраска! Также раскраска может содержать параллельные комментарии и задания другого типа (посчитай и раскрась, собери предметы и раскрась и т.д.).
Посчитай, сколько мишек на картинке.
Можно предложить малышу книжку о цифрах в картинках. Также может пригодиться красочная презентация. Она отлично подойдет и для учителей, которые идут к детям на урок в 1 класс. Презентация с комментарием на русском языке даст возможность ребятам выстроить ассоциативный ряд с цифрой. Презентация может заключать в себе некоторые фото предметов, явлений, связанных с цифрой 3.
Также следует помнить, что существует еще римская цифра 3. Это число также может быть представлено в картинках.
Языковые методы изучения
Прекрасным подспорьем на уроках математики, если учитель идет на урок в 1 класс, могут стать стихи, пословицы, поговорки, загадки. Стихи можно предложить выучить одному ученику, который потом расскажет их на уроке. Стихи про цифру 3 есть у многих авторов, в том числе современных. Наиболее известны стихи С. Маршака «Веселый счет». Эти стихи также помогут ребенку выстроить ассоциативный ряд с цифрой.
Интересен будет вопрос для ребят, которые посещают детский сад или 1 класс: что означает число 3? А ведь действительно, неужели число что-то означает?
В древности люди верили, что число 3 означает нечто магическое, совершенное. Это число идеала, совершенства, святыни, не только в язычестве, но и в христианстве. Помните: 3 означает святую Троицу, а в сказках есть троекратные повторы. Наверняка ребенок на такой вопрос скажет, что число 3 означает семью, три колеса велосипеда и т.д. Он будет исходить из собственного опыта. Расширьте его представления, используя поговорки, пословицы, загадки.
Стихи Маршака про цифры.
Пословицы на русском языке просто пестрят упоминаем этого священного числа. Кроме того, пословицы часто обладают назидательным смыслом, и услышать их малышу будет не лишним. Пословицы часто представляют тройку в ее сакральном значении: именно исконно русские корни, присутствующие в фольклоре, могут по-настоящему воспитать детей.
Подборка пословиц и поговорок про цифру 3 для детей.
Особый вид творчества представляют собой загадки. Это короткие строчки, в которых зашифровано число 3. Загадки не только дают возможность выстроить ассоциации, но и развивают смекалку. Используйте загадки для дошкольников и детей, посещающих 1 класс. Они станут сообразительнее и будут мыслить быстро и творчески.
Раскраски
Визуальные пособия
Украсить урок, если вы идете в 1 класс, разнообразить занятия в детском саду может презентация или фото. Презентация поможет детям быстрее запомнить, как выглядит число 3, на что оно похоже, что означает. Презентация содержит интересные фото предметов. Можно разложить фото перед ребенком и попросить посчитать их количество. Также фото помогут, если надо выяснить, на что похожа цифра.
Презентация поможет детям быстрее запомнить, как выглядит число 3, на что оно похоже, что означает. Презентация содержит интересные фото предметов. Можно разложить фото перед ребенком и попросить посчитать их количество. Также фото помогут, если надо выяснить, на что похожа цифра.
Итак, давайте детям больше творческих заданий, даже если они связаны с таким сухим и прагматичным предметом, как математика. В числах тоже можно отыскать элемент новизны.
Веселые задания
Что нужно сделать?
- Посчитать инопланетян (их трое).
- Найти цифру три среди других цифр.
- Посчитать количество предметов и написать ответ в кружке (их будет по 3).
- Обвести несколько раз большую цифру 3.
- Провести линию и найти все цифры 3, спрятавшиеся в сердечках.
- Подрисовать пчёл к улею.
- Найти и раскрасить цифру три спрятавшуюся на картинке с бабочкой.
Вот и сами задания:
Пакет увлекательных заданий для детей о цифре три.
Прописи
Очень хороший видео урок для деток из Арифметики малышки о цифре три от тётушки совы. Посмотрите обязательно).
Стихи про цифру 3
Нет, ты только посмотри,
Как красива цифра три!
Стоит лишь два полукруга
Нам поставить друг на друга.
Цифра три невелика,
Но везде она нужна.
В светофоре три огня,
И в упряжке три коня.
В сказках есть три толстяка, три девицы
И три дня скакал Иван
По лесам и по полям.
В тридесятом государстве
Он царевну отыскал.
На картине Васнецова
Трех богатырей мы видим снова.
И в пословицах, загадках
Цифра три звучит в отгадках.
Только в школе не всегда
И не всем она нужна.
Мы хотим оценку “пять”
Вместо тройки получать.
Не сидит без дела Тройка,
Затевает тройка стройку.
Тройка главный командир,
И прораб, и бригадир!
Три веселых комара
Тащат краски три ведра,
Пилят доски три грача,
Волк несет три кирпича.
С молотками три котенка,
Гвозди носят три утенка.
Три крота траншею роют,
Три медведя крышу кроют.
Три козы сложили печку,
Красят окна три овечки.
Каждый зверь пришел, помог:
Получился теремок!
Две подковки — посмотри —
Превратились в цифру 3.
У леса на опушке,
Там, где растут дубы,
3 белки без просушки
Развесили грибы.
Украсили полянку
Гирляндами опят —
Супы готовить станут
Зимою для бельчат.
Тройка — третий из значков,
Состоит из двух крючков.
Три размера есть:
Длина,
Высота и ширина.
Время
На три делят люди:
Что прошло,
Что есть,
Что будет.
Но важней всего семья:
Трое:
Папа, мама, я!
А вот это — посмотри,
Выступает цифра три.
Тройка — третий из значков —
Состоит из двух крючков.
На картонке – три картинки:
На одной картинке – кот,
На другой картинке – кринка,
А на третьей на картинке
Чёрный кот из жёлтой кринки
Молоко лакает-пьет.
Автор: Е.А.Благинина
Бежит по снегу Зайка,
За ним – собака Лайка,
З ней бежит хозяйка,
И все втроем бегут!
Сейчас догонит Лайка
Тебя, несчастный Зайка, —
И подберёт хозяйка
Твой хвостик на снегу!
Погляди на цифру 3 —
Точно ласточка, смотри.
Автор: Г. Виеру
У старинушки три сына:
Старший умный был детина,
Средний сын и так и сяк,
Младший вовсе был чудак.
Братья сеяли пшеницу
Да возили в град-столицу:
Знать, столица та была
Недалече от села.
Третья цифра — это три.
Хорошенько посмотри:
Это твой велосипед
На земле оставил след.
Ну-ка, сколько здесь полос?
Ну-ка, сколько здесь колес?
Автор: С.Я. Маршак
Мельник с единственным сыном
По лесу однажды шли.
Вдруг видят они – три голубки
Вспорхнули и скрылись вдали.
Третий звонок,
Дон-дон-дон!
Пассажиры, кошки и куклы,
В вагон!
До свидания, пишите!
Машите платками, машите!
Машинист, свисти!
Паровоз, пыхти!
3 — это заклинатель змей
Вышел с дудочкой своей.
Перед ним танцует змейка —
Хвост крючком, дугою шейка.
Ты на змейку посмотри —
Да ведь это цифра три!
Автор: В. Данько
«Три очка за старичка»
Стоит Лариса у доски,
Девчонка в пышной юбке,
И переводит на очки
Хорошие поступки.
Вся в цифрах классная доска.
— За помощь маме — два очка,
За помощь брату-малышу
Очко Никитину пишу,
А Горчакову три очка —
Водил он в гости старичка.
— За это мало трёх очков!—
Кричит Андрюша Горчаков
И вскакивает с лавки.—
Три очка за старичка?!
Я требую прибавки!
Я с ним провёл почти полдня,
Он полюбить успел меня.
Автор: Агния Барто
Пошёл Серёжа в первый класс,
С Серёжей не шути!
Считать умеет он у нас
Почти до десяти!
Не грех такому мудрецу
Задрать курносый нос:
Вот как – то за столом отцу
Он задаёт вопрос…
Два пирожка тут, папа, да?
А хочешь, на пари,
Я доказать могу всегда,
Что их не два, а три!
Считают вместе.
Вот один, а вот и два. Смотри!
Один да два…
Закончил сын…
Как раз и будет три!
Вот молодец!
Сказал отец.
И в самом деле три!
И потому я два возьму,
А третий ты бери!
А в третьем вагоне – возня, суета:
Ватага ребят занимает места.
Они повторяют во время движенья
Сложенье, деленье, склоненье, спряженье.
Смотрите также:
Факты о цифре 3
Сегодня давайте взглянем на интересные факты о цифре 3.
На протяжении веков люди приписывали множество фактов числам.
Нумерология, суеверия, важные даты и многое другое цепляются за различные числа, что в некоторых случаях придает им большое значение!
Почему цифра 3 так распространена в нашей повседневной жизни, истории, суевериях и культуре?
- Цифра 3 с древних времен на Руси считалось сакральным. Излюбленное в русских народных сказках: три богатыря, медведя, желания, дороги, три попытки. У царя или мужика было 3 сына. Жили в тридевятом царстве, в тридесятом государстве. Сражались с трехглавым Змей-Горынычем и т.д. Можно составить длинный список.
- В глубокой старине думали, что Земля держится на трех китах, или трех слонах.
- В христианстве четыре олицетворяет тело, цифра 3 – душу. Оно знаменует Божественное Триединство. В связи с этим фактом в православии к одному из известных праздников относится День Святой Троицы, приходящейся на 50-й день от Пасхи. Апостол Петр отрекся трижды.
- Основные христианские добродетели — Вера, Надежда, Любовь. 30 сентября – День этих святых, юных великомучениц и их матери Софии, не отрекшихся от веры под пытками.
- Католики отмечают праздник «Трех царей» в честь поклонения волхвов. Индуизм опирается на правящих богов. И здесь не обошлось без цифры 3: Брахма — Создатель, Вишну — охранитель, Шиву – Разрушитель, именуемые Тримурти.
- И спорт не обошелся без цифры 3.Играя в бейсбол, отбивающий выбывает из матча, если наносит удар трижды. Подобный факт называется аутом, когда удар означает, что отбивающий не смог ударить по мячу при правильной подаче.
Цифра 3 представляется счастливой в китайской культуре. Причина – звучание слова, обозначающего число, очень похоже на слово «живой».
- В скандинавской мифологии говорится: перед Рагнароком будет 3 невероятно суровых зимы подряд. Рагнарок — период, когда происходит великая битва, навсегда меняющая облик мира. Главные скандинавские боги погибают, а мир создается заново.

- Термин «хет-трик» используется во многих различных видах спорта. Факт тот, что каждое значение имеет отношение к цифре 3. В крикете, например, боулер сделал хет-трик, если он выбил (выбывает из игры) 3 бьющих в 3-х последовательных бросках. В футболе, хоккее – когда игрок забивает 3 гола.
- Атомный номер химического элемента лития равен трем. В нормальных условиях литий приобретает серебристо-белый цвет. Этот щелочной металл — самый легкий из металлов и легко воспламеняется. Одно из самых часто встречающихся мест, где вы найдете литий, — литиевые батареи.
- В индийской астрологии цифра 3 символизирует планету Юпитер. Юпитер — планета удачи, милосердия, оптимизма и благополучия.
Интересный факт выбранный Многознайкой
А сколько пословиц, поговорок, загадок с цифрой 3! Заблудился в трёх соснах. Из третьих уст, из третьих рук. Наговорил с три короба. Три жены имел, от всех терпел. Если у одной плиты три повара толкутся — обед пригорает. За двоих попотеешь — за троих поешь.
- Большинство цветов, которые способны видеть люди, получаются из комбинации трех цветов. В данном случае они являются основополагающими. Для разных целей используются различные основные цвета. Неоспоримый факт, что смешивая краску, вы сможете получить почти любой оттенок, смешав синий, желтый и красный пигменты. С другой стороны, цвета в телевизоре состоят из комбинации красного, зеленого и синего.
- Всё, что называется трехмерным, занимает пространство в трех разных измерениях. Например, квадрат, нарисованный на листе бумаги, имеет два измерения — длину и ширину. Кубик, который можно держать в руке, трехмерен: имеет длину, ширину и высоту!
- Считается несчастливым зажечь 3 сигареты одной спичкой. Истоки суеверия довольно сильно различаются. Наиболее распространенным из возможных источников является Первая мировая война. Исторический факт заключается в следующем: если снайпер заметит солдата в окопах закуривающего сигарету, он будет предупрежден.
 Ко времени закуривания второго он нацелил свою снайперскую винтовку. Третий человек, который закурит сигарету, будет застрелен, поскольку у снайпера было достаточно времени для подготовки. Правдиво или нет, суеверие прижилось.
Ко времени закуривания второго он нацелил свою снайперскую винтовку. Третий человек, который закурит сигарету, будет застрелен, поскольку у снайпера было достаточно времени для подготовки. Правдиво или нет, суеверие прижилось. - Разработали новый способ записи цифры 3 для предотвращения путаницы и потенциальной подделки. Данный вариант цифры 3 имеет плоскую вершину и создан таким образом, чтобы не могли легко заменить на восемь.
Установленный факт, что в ранней цивилизации, когда люди впервые учились считать, существовало слово только для одного, двух, трех. Большая часть свидетельств, подтверждающие эту теорию, исходит из методов подсчета, используемых в племенах джунглей Амазонки. Интересный факт: аборигены Полинезии считают так: один, два, три, много.
- Некоторые относят его к несчастливым, другие наоборот – удачным.
- Третье место не так хорошо, как первое или второе — факт. Но набрать 3 очка в отдельных видах спорта –не плохо и даже замечательно!
Видеть положительные стороны цифры 3 вместо возможных отрицательных гораздо интереснее. Поэтому негатив не ищем!
ПОНРАВИЛАСЬ СТАТЬЯ-ПОДЕЛИСЬ С ДРУЗЬЯМИ! НАЖМИ НА КНОПКУ НИЖЕ!
Предыдущая статьяРедкий вид хамелеона Воельцкова, исчезнувший 100 лет назад, снова замеченСледующая статьяЖивотное Кенгуру-все самое интересное о сумчатом символе загадочной Австралии
Цифры на английском языке. Считаем без труда!
Без чего не может обойтись человек, начинающий изучать английский? Что должен выучить ваш ребенок к школе? Без чего вы даже не можете сказать, который час сейчас? Конечно же, без цифр. Выучить цифры на английском языке довольно-таки просто. Можно заучивать их с помощью интересных цветных картинок, можно петь как песню, можно запоминать как скороговорку – простор для фантазии и творчества!
Как назвать цифры на английском языке
Перечислим основные цифры на английском языке:
- 0 – zero – ноль;
- 1 – one – один;
- 2 – two – два;
- 3 – three – три;
- 4 – four – четыре;
- 5 – five – пять;
- 6 – six – шесть;
- 7 – seven – семь;
- 8 – eight – восемь;
- 9 – nine – девять.

Не поддаются общим правилам образования такие числа:
- 10 – ten – десять;
- 11 – eleven – одиннадцать;
- 12 – twelve – двенадцать;
- 100 – hundred – сто;
- 1000 – thousand – тысяча.
Как правильно произносить их на английском языке?
Правильно произносить цифры, да и все остальные слова английского языка можно, только зная транскрипцию. Транскрипция – это особая запись слова так, как оно произносится (например, русское слово «рисоваться» транскрипционно можно записать как [рисаваца]). Да и учить английские цифры с транскрипцией гораздо легче, чем без нее.
Вот как читаются английские цифры:
- 0 – 🔊 Слушать
zero – [‘ziərəu];
- 1 – 🔊 Слушать
one – [wʌn];
- 2 – 🔊 Слушать
two – [tu:];
- 3 – 🔊 Слушать
three – [θri:];
- 4 –🔊 Слушать
four – [fɔ:];
- 5 –🔊 Слушать
five – [faiv];
- 6 – 🔊 Слушать
six. – [siks];
- 7 – 🔊 Слушать
seven – [‘sev(ə)n];
- 8 – 🔊 Слушать
eight – [eit];
- 9 – 🔊 Слушать
nine – [nain];
- 10 – 🔊 Слушать
ten – [ten];
- 11 – 🔊 Слушать
eleven – [i’lev(ə)n];
- 12 – 🔊 Слушать
twelve – [twelv];
- 100 –🔊 Слушать
hundred – [hʌndred];
- 1000 – 🔊 Слушать
thousand –[θʌuzend].
Но что делать, если вы не знаете, как читается транскрипция? Для тех, кто только-только собирается с нуля выучить английский, цифры с русской транскрипцией очень пригодятся:
- 0 – zero – [зироу];
- 1 – one – [уан];
- 2 – two – [ту];
- 3 – three – [сри];
- 4 – four – [фо];
- 5 – five – [файв];
- 6 – six – [сикс];
- 7 – seven – [севен];
- 8 – eight – [ейт];
- 9 – nine – [найн];
- 10 – ten – [тен];
- 11 – eleven – [илевен];
- 12 – twelve – [твелв];
- 100 – hundred – [хандред];
- 1000 – thousand – [саузенд].

Все возможные числа, самые большие, которые только можно себе представить – это всего лишь комбинации девяти цифр, от нуля до девяти. Числа образуются по особым правилам.
Правила образования чисел в английском
Вообще числа в английском можно разделить на:
• простые;
• производные;
• составные.
Понять, какое число каким является, очень просто. Простые состоят из одного слова (например: five, nine, thousand). Производные состоят из одного слова, но при этом имеют суффиксы –teen (от 13 до 19) или –ty (десятки от 20 до 90). Составные же, как следует из их названия, состоят из нескольких числительных.
Как образовать производные числительные?
Чтобы образовать производные числительные от 13 до 19, возьмите число от 3 до 9 и добавьте к нему суффикс –teen. Некоторые буквы при этом могут меняться! Будьте внимательны!
13 – three + teen = thirteen;
14 – four + teen = fourteen;
15 – five + teen = fifteen;
16 – six + teen = sixteen;
17 – seven + teen = seventeen;
18 – eight + teen = eighteen;
19 – nine + teen = nineteen.
Ударение в этих числительных будет падать на суффикс. Читаются числительные сообразно с транскрипцией первых частей (например: fifteen – [фифтин], eighteen – [ейтин]).
Чтобы образовать производные числительные от 20 до 90, возьмите число от 2 до 9 и добавьте к нему суффикс –ty.
20 – two + ty = twenty;
30 – three + ty = thirty;
40 – four + ty = forty;
50 – five + ty = fifty;
60 – six + ty = sixty;
70 – seven + ty = seventy;
80 – eight + ty = eighty;
90 –nine + ty = ninety.
Ударение в этих числительных будет падать на корень. Читаются так же, как первые части: (например: sixty – [сиксти], forty – [фоти]).
Как образовать составные числительные?
Составные числительные образуются с помощью десятков + единиц (если число меньше ста), сотен + десятков + единиц (если число меньше тысячи) и т. д.
д.
Например, вы хотите образовать число «двадцать один». Вам нужно написать два слова: «двадцать» и «один». Таким образом, twenty-one– это и будет двадцать один! При этом двузначные числа пишутся через дефис.
Аналогично можно образовать любые числа до сотни:
Пятьдесят три – fifty + three = fifty-three.
Сорок девять – forty + nine = forty-nine.
Семьдесят два – seventy + two = seventy-two.
Тридцать шесть – thirty + six = thirty-six.
Девяносто девять – ninety + nine = ninety-nine.
Чтобы образовать любое число до тысячи, необходимо указать число сотен + десятков + единиц, при этом после числа сотен пишется and (британский английский), а далее двузначное число через дефис:
Сто двадцать один – one hundred and twenty-one.
Пятьсот сорок три – five hundred and forty-three.
Двести два – two hundred and two.
Триста пятьдесят восемь – three hundred and fifty-eight.
Четыреста – four hundred.
Аналогично и с большими числами. Произносятся они так же, как и их части.
Вот и все – теперь вы знаете английские цифры, можете правильно их читать и составлять из них числа. Хоть запомнить сразу все цифры и правила их образования достаточно сложно, это не должно вас отталкивать. Ищите разные скороговорки, стишки, песни, смотрите обучающие видео — в общем, в обучении, как и на войне, все средства хороши! Удачи вам в изучении английского языка!
Статья рекомендована экспертом: Мария Соломатина
2- и 3-значное умножение
В этом посте мы рассмотрим , чтобы узнать, как умножать на двузначные и трехзначные числа .
Прежде чем мы начнем, давайте рассмотрим, что такое члены умножения :
- Факторы: Факторы — это числа, которые умножаются.
- Произведение: Произведение является результатом умножения.
- Множаемое: Множаемое — это число (множитель), которое умножается.

- Множитель: Множитель — это число (множитель), на которое вы производите умножение.
Обычно первым записывается множитель с большим числом цифр. Обычно множимое больше множителя.
Теперь посмотрим, что такое шагов для умножения на двузначные и трехзначные числа .
Первый шаг: Умножьте единичную цифру нижнего множителя (множителя) на верхний множитель (множимое) и запишите результат в строке ниже.
Давайте посмотрим на пример. Если мы умножаем 781 x 95, первое, что нужно сделать, это умножить на 5, что находится в разряде единиц 95, на каждую из цифр верхнего множителя справа налево и поместить результат 3905 на строку ниже, как показано на изображении.
Второй шаг: Умножьте цифру в разряде десятков нижнего множителя на верхний множитель и запишите результат в строке ниже, но поставьте 0 в разряде единиц, так как эта часть умножения является числом десятков.Продолжим пример. Теперь мы умножаем 9, учитывая, что оно находится в разряде десятков нижнего множителя 95, на верхний множитель 781. Результат, 7029, должен быть записан под 3905, но перемещен на одну позицию влево.
Третий шаг: Добавьте продукты. Как мы видим на изображении, мы складываем продукты, и результат умножения равен 74,195.
Если нижний коэффициент (множитель) представляет собой трехзначное число , то за результатом умножения разряда сотен будут два 0.Давайте посмотрим на другой пример. Если мы умножаем 367 x 251, первое, что нужно сделать, это умножить цифру в разряде единиц 251, то есть 1, на 367. Результатом будет 367, и мы поместим его в строку ниже.
После того, как мы умножим цифру в разряде десятков 251, то есть 5, на 367. Результатом будет 1835, и мы поместим его в строку ниже, а вместо единиц поставим 0.
Затем мы умножаем цифру в разряде сотен 251, то есть 2, на 367.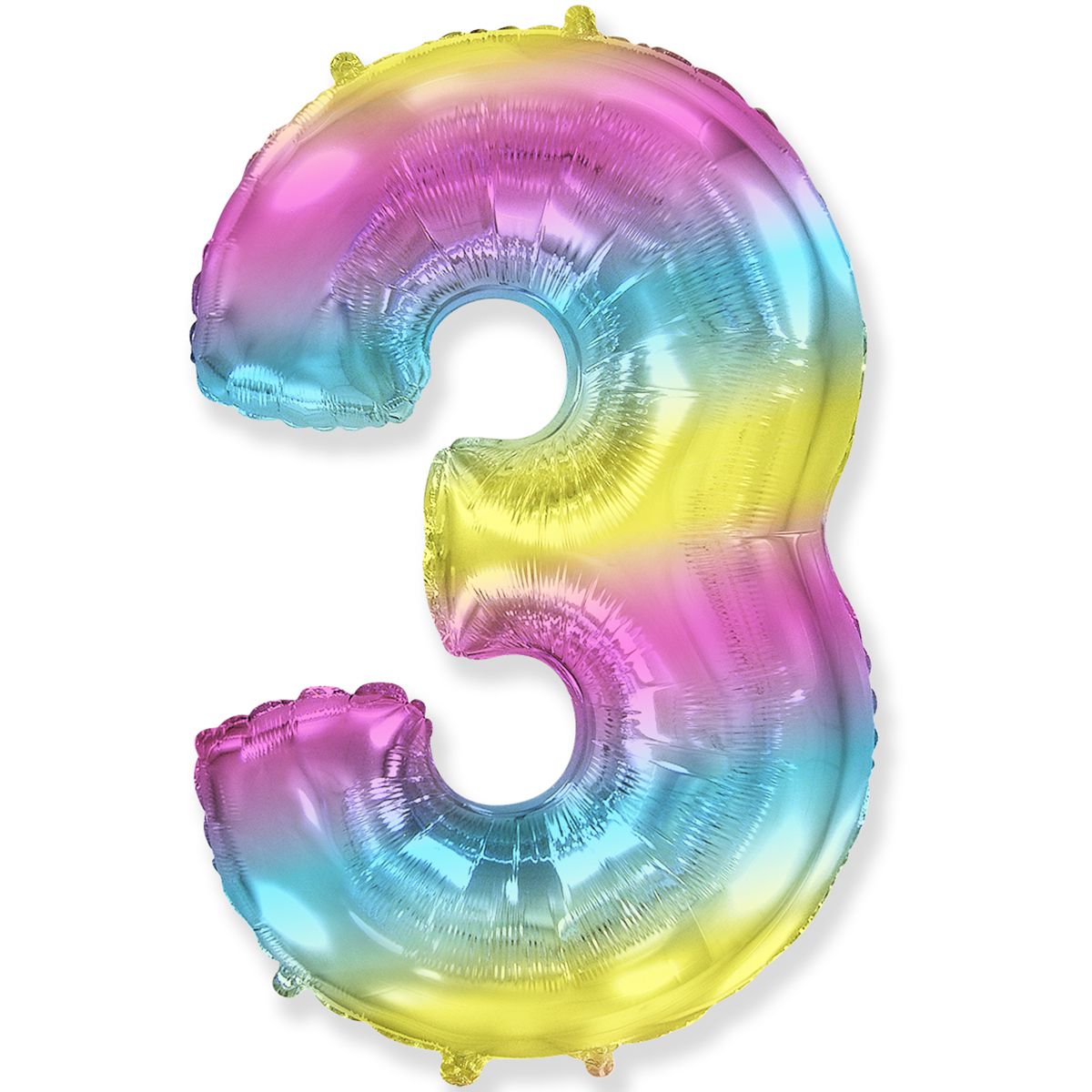 Результатом будет 734, и мы поместим его в строку ниже, за которой следует 0 в разрядах десятков и 0 в разрядах единиц. место.
Результатом будет 734, и мы поместим его в строку ниже, за которой следует 0 в разрядах десятков и 0 в разрядах единиц. место.
Наконец, мы производим сложение, и получаем результат 92,117.
Если вы хотите попрактиковаться в умножении на 2- и 3-значные числа и заняться более элементарной математикой, попробуйте Smartick бесплатно!
Подробнее:
Команда по созданию контента.
Многопрофильная и многонациональная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать максимально возможное математическое содержание.
NumberNut.com: Арифметика: Умножение: трехзначные числа
Вау.Вы можете использовать до трехзначных чисел для умножения. Давайте посмотрим на наши возможные варианты и рассмотрим пример для каждого из них. Не забывайте добавлять ноль (и) в конце чисел при умножении на двух- или трехзначный множитель. Используйте один ноль для значения десятков, два нуля для значения сотен и т. Д. Ознакомьтесь с нашей страницей по умножению на двузначные числа для объяснения.
Пример:
Трехзначное число, умноженное на однозначное число (без переноса):
123 x 3 =?
(1) 3 x 3 = 9 (единицы)
(2) 2 x 3 = 6 (десятки)
(3) 1 x 3 = 3 (сотни)
Ответ: 123 x 3 = 369
Пример:
Трехзначное число, умноженное на двузначное число (без переноса):
424 x 12 =?
Часть I (424 x 2):
(1) 4 x 2 = 8
(2) 2 x 2 = 4
(3) 4 x 2 = 8
Ответ: 424 x 2 = 848
Часть II (424 x 1):
(1) 4 x 1 = 4
(2) 2 x 1 = 2
(3) 4 x 1 = 4
Ответ: 424 x 1 = 424
Часть III (848 + 4240 [мы добавили ноль]):
848 + 4240 = 5 088
Можно написать так…
Пример:
Трехзначное число, умноженное на трехзначное число (без переноса):
213 x 332 =?
Часть I (213 x 2):
(1) 2 x 2 = 4
(2) 1 x 2 = 2
(3) 3 x 2 = 6
Ответ: 213 x 2 = 426
Часть II (213 x 3):
(1) 2 x 3 = 6
(2) 1 x 3 = 3
(3) 3 x 3 = 9
Ответ: 213 x 1 = 639
Часть III (213 x 3):
(1) 2 x 3 = 6
(2) 1 x 3 = 3
(3) 3 x 3 = 9
Ответ: 213 x 1 = 639
Часть IV (426 + 6390 + 63900 [мы добавили нули]):
426 + 6390 + 63900 = 70 716
Когда писали когда-то. ..
..
| 213 x 332 426 639 0 + 639 00 70716 |
Иногда мы расстраиваемся, выполняя длинные задачи на умножение . Это не очень захватывающе и очень однообразно. Но чтобы получить правильный ответ, вам нужно придерживаться процесса , процесса . Если вы пропустите шаг или ошибетесь в простом сложении, вы получите неправильный ответ. Вы также, вероятно, потеряете несколько очков на тесте.Просто будьте пациентом , когда вы работаете над тремя задачами умножения и переносом / перегруппировкой значений в задаче с большими числами. Арифметика легко, когда вы знаете основы. Неважно, как выглядят числа или насколько они велики.
Вы должны привыкнуть к этому сейчас. По мере изучения математики числа будут становиться больше. Это не плохо и не страшно. Почему? Вам не о чем беспокоиться, потому что вы будете знать основные шаги для решения любой задачи умножения.Вам могут дать число в сотнях (100+) или число в триллионах (1 000 000 000 000+), и вы будете знать, как получить ответ. Не ждите, что быстро решите большое количество проблем. На это уйдет больше времени, но не сложнее. Как всегда, не забывайте практиковать умножение.
Что такое числа до 3-х знаков?, Решенные примеры и практические задачи.
Номера широко классифицируются в зависимости от количества цифр. Здесь мы рассмотрим трехзначные числа, их формирование и важность чисел и разрядов.Цифры, используемые для образования более высоких цифр, — это 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Разрядное значение трехзначного числа помогает понять значение каждой из цифр. Наименьшее из трехзначных чисел — 100, а наибольшее — 999.
Изучение 3-значных чисел — это строительный блок для чисел с более высокими цифрами. Здесь мы узнаем больше о важности, образовании и значении числа в числах до трехзначных чисел.
Разрядное значение трехзначных чисел
Значение каждого трехзначного числа можно найти, посмотрев, какое разрядное значение имеет каждая цифра.Давайте рассмотрим число 243. Говорят, что первая цифра в крайнем правом положении стоит на месте единиц, поэтому они будут умножены на 1. Следовательно, произведение равно 3 × 1 = 3. Тогда второе число равно 4, и потому что оно находится на разряде десятков, оно умножается на 10. Следовательно, значение равно 4 × 10 = 40. Третье число 2 находится на разряде сотен. Итак, 2 умножается на 100, и его значение равно 2 × 100 = 200. Следовательно, число равно 200 + 40 + 3 = 243.
Разложение трехзначного числа : В трехзначном числе используются три разряда — сотни, десятки и единицы.Давайте возьмем один пример, чтобы лучше понять это. Здесь 465 — это трехзначное число, которое разложено в виде суммы трех чисел. Так как 5 находится на месте единицы, 60 — на разряде десятков, а 400 — на разряде сотен.
Значение нуля в трехзначных числах: Нулевое число не вносит никакого вклада в трехзначное число, если оно помещено в позицию, где нет других ненулевых чисел слева от него. Так чем же 303 отличается от 033 или даже от 003? В 033 значения равны 0 × 100 + 3 × 10 + 3 × 1 = 0 + 30 + 3 = 33, что означает, что число фактически становится двузначным числом 33, или в случае 003 оно становится однозначным. цифра номер 3.В этих двух примерах нулевые цифры не добавляют никакого значения к числу, поэтому числа также могут быть выражены как 33 или 3.
Расширенная форма трехзначных чисел
Трехзначное число в расширенной форме можно выразить и записать тремя различными способами. Рассмотрим трехзначное число 457. Число 457 может быть записано в одной форме как 457 = 4 × сотни + 5 × десятки + 7 × единицы. Во втором случае число 457 можно записать как 457 = 4 × 100 + 5 × 10 + 7 × 1.И, наконец, число 457 может быть расширено в виде 457 = 400 + 50 + 7. Все три способа записи чисел в развернутой форме верны. Написание трехзначного числа в развернутом виде помогает узнать составляющие числа.
Обычно разделение или расширение трехзначного числа помогает нам лучше понять трехзначное число. При разделении мы узнаем количество сотен, десятков и единиц, доступных в трехзначном числе.
Давайте рассмотрим некоторые из нижеупомянутых важных моментов, касающихся 3-значных чисел.Это помогает лучше понять 3-значные числа.
- 100 — наименьшее трехзначное число, а 999 — наибольшее трехзначное число.
- Трехзначное число не может начинаться с 0.
- 10 десятков составляют 1 сотню, которая является наименьшим трехзначным числом, а 10 сотен составляют тысячу, которая является наименьшим четырехзначным числом.
Распространенные ошибки при вводе чисел до 3-х цифр
Некоторые из типичных ошибок наблюдаются при написании или чтении 3-значного числа.Эти ошибки в чтении и интерпретации 3-значного числа часто понимают как какое-то другое число. В процессе чтения, записи и интерпретации трехзначного числа разрядное значение цифр должно интерпретироваться правильно. Ниже мы перечислили три распространенные ошибки, которые часто совершают дети при написании трехзначных чисел.
- Заблуждение 1 : Дети ошибаются при определении чисел, когда единица равна нулю, а разряды десятков . Пример: Когда учеников попросят прочитать 130 и 103, они могут запутаться. Это помогает им моделировать числа с помощью блоков Base-10. Таким образом они смогут ясно увидеть десятичные и единичные значения.
- Заблуждение 2 : Когда студентов просят написать «сто двадцать три», студенты часто сначала пишут 100, а затем добавляют к нему 23, в результате чего получается число «10023» Факт: Это заблуждение возникает из-за поверхностное понимание пространственных ценностей.Используя блоки с основанием 10 или счеты, покажите детям, что цифра имеет разные значения в зависимости от ее положения.
- Заблуждение 3 : Иногда , когда их просят образовать наименьшее трехзначное число из трех цифр, включающих ноль, дети помещают ноль в крайнее левое положение . Факт: Это неверно. Если мы создаем трехзначное число, ноль не может быть в разряде сотен. например Наименьшее трехзначное число, состоящее из всех цифр 5, 0 и 7, — это 507, а не 057
.
Операции с числами до 3-х цифр
Четыре арифметические операции сложения, вычитания, умножения и деления могут быть удобно выполнены с 3-значными числами.В процессе выполнения этих арифметических операций значение разряда соответствующего числа должно быть правильно согласовано. Ошибка при сопоставлении разряда может привести к неправильным ответам. Здесь мы рассмотрим простое упражнение с использованием 3-значных чисел, чтобы помочь нам понять закономерность изменения каждой из цифр сотого разряда, разряда десятков и разряда единиц. Это упражнение поможет лучше понять обучение, необходимое для 3-значных чисел.
Попросите учащихся пропустить счет на 10 и 100, чтобы научиться бегло говорить с 3-значными числами .Сначала начните с 100. Затем начните с любого случайного трехзначного числа, например 136.
Помогите детям определить закономерность, согласно которой при пропуске счета на 10 цифра в единичном значении не меняется. Аналогично, при пропуске счета на 100, цифры в разряде единиц и разряда десятков не меняются .
Используйте сетку из 100 квадратов, чтобы повысить беглость . Предложите учащимся определить закономерность, согласно которой перемещение на одну строку вверх или вниз равносильно пропуску счета на 10.Перемещение столбцов (влево или вправо) увеличивает или уменьшает числа на 1.
Часто детям дают три цифры и просят найти наибольшее и наименьшее число из трех цифр, используя все цифры. Хитрость здесь в том, чтобы расположить все цифры в порядке убывания, чтобы найти наибольшее число.
Чтобы найти наименьшее число, расположите все цифры в порядке возрастания . Но учтите, что если ноль — одна из цифр, его нельзя ставить слева.Например. Используя цифры 7, 3 и 6, наибольшее число составляет 763 (цифры в порядке убывания), а наименьшее число — 367 (цифры в порядке возрастания). Используя цифры 4, 0 и 8, наибольшее число будет 840, но наименьшее трехзначное число будет 408, а не 048.
Часто задаваемые вопросы о номерах до 3-х цифр
Сколько всего трехзначных чисел?
Всего 900 трехзначных чисел. К ним относятся наименьшее трехзначное число — 100 до наибольшего трехзначного числа — 999.Цифры за этими 3-значными числами являются 4-значными числами, а числа меньше 3-значных чисел являются 2-значными числами.
Какое наибольшее трехзначное число?
Наибольшее 3-значное число — 999. Если добавить к нему еще 1, получится 4-значное число.
Какова сумма трех наибольших трехзначных чисел?
Три самых больших трехзначных числа: 997, 998, 999. Их сумма равна 2994, так как 997 +998 +999 = 2994.
Как научить трехзначное число?
Трехзначные числа можно сначала научить, понимая их разрядные значения.Далее нам нужно знать ограничения использования чисел в каждом значении разряда. В трехзначном числе цифра ноль не может быть помещена в сотню.
Какое наименьшее трехзначное число?
Число 100 — это наименьшее трехзначное число. Если вычесть 1, получится двузначное число. Всего существует 900 трехзначных чисел, из которых число 100 является наименьшим трехзначным числом.
Как суммировать трехзначные числа?
Сумма 3-значных чисел такая же, как сумма 2-значных или более высоких цифр.Единственное условие — сумма цифр в определенном месте переносится на следующую позицию. Сумма цифр разряда единиц переносится в разряды десятков, а сумма разрядов разряда разрядов переносится в разряды сотых.
Сколько существует четных трехзначных чисел?
Всего 900 3-значных номеров. Из них половина — четные, а оставшаяся половина — нечетные. Следовательно, есть 900/2 = 450 четных трехзначных чисел.
Может ли трехзначное число содержать два нуля?
Трехзначное число может иметь два нуля. Два нуля должны быть на месте десяти и единицы. Некоторые из примеров трехзначных чисел — это 100, 200, 300, 400. Единственное необходимое условие — то, что ноль не может быть на сотом месте.
Умножение одной цифры на трехзначные числа — математика для 3-го класса
Узнайте, как умножить одну цифру на трехзначные числа
Итак, вы научились умножать однозначное число на двузначное.
В этом уроке мы собираемся научиться умножать однозначные числа на трехзначные числа . 😃
Умножение 1 цифры на 3 цифры
Это похоже на умножение двузначных чисел, но с дополнительным шагом в конце. 😎
Вот шаги, описанные в одном предложении:
Когда умножает 1-значное число на 3-значное число , умножьте однозначное число на каждую из цифр 3-значного числа, начиная с Единицы разряда .
Итак, приступим.
Допустим, у вас есть такое уравнение:
310 x 2 = ?
👉 Первое, что вам нужно сделать, это расположить числа в форме столбца .
Так будет проще умножать числа.
😀 Совет: напишите 3-значное число вверху, и 1-значное число внизу.
👉 Убедитесь, что выровняли 2 с 0. Обе цифры находятся в разряде единиц.
Итак, давайте еще раз рассмотрим шаги:
Когда умножает 1-значного на 3-значное число, умножает 1-значное число на каждую из цифр 3-значного числа, начинается с единицы .
Сначала умножаем 2 x 0.
Помните наше правило умножения на 0? 😉
Ответ всегда 0.
2 x 0 = 0
👉 Напишем 0 вместо Ones.
Далее, умножить 2 x 1.
Наше правило умножения на 1 очень просто!
Ответ тот же номер.
2 x 1 = 2
👉 Напишем 2 в разряде Десятки.
Затем умножить 2 x 3.
Какое правило умножения на 3?
Да!
Просто удвойте число и добавьте еще одну группу.
2 x 3 = 6
👉 Пишем 6 в месте Сот.
Итак, 310 x 2 = 620 .
Другой пример
Давайте решим еще одно уравнение.
758 x 4 = ?
Прежде чем что-либо умножать, мы должны сначала расположить числа в столбце из .
Теперь мы готовы!
Сначала умножаем на 4 х 8.
4 x 8 = 32
Что нам делать, когда у нас есть двузначный ответ?
👉Мы переносим в первую цифру в столбец Десятки.
👉 2 находится на месте Единиц, и мы перенесли 3 в столбец Десятки.
😃 Совет: Мы хотим убедиться, что есть место для следующего ответа, поэтому мы переносим на цифры.Это ведь не «нести вниз», правда?
Что нам делать дальше?
Далее, , мы умножаем на 4 x 5, и прибавляем 3 , которое мы перенесли через после !
4 x 5 = 20
Это дает нам 20.
Теперь, когда мы умножили, мы добавляем 3, которые мы перенесли.
20 + 3 = 23
😃 Мы знаем, что нельзя записать 23 в разряде десятков.
Если мы это сделаем, то для следующего ответа не останется места.
👉 Итак, мы записываем 3 на место Десятки, и переносим 2 в столбец Сотен.
Наконец, умножаем 4 x 7.
4 x 7 = 28
… но мы перенесли 2 в столбец Сотни на последнем шаге.
👉 Итак, мы должны добавить это к 28.
28 + 2 = 30
Поскольку у нас нет других чисел для умножения позже, мы можем написать обе цифры в нашем ответе.
Итак, 758 x 4 = 3,032 .
Смотри и учись
Вы можете сразу приступить к практике!
3-значное умножение на 2-значные рабочие листы
Рабочие листы
В этом рабочем листе умножения 3-значное на 2-значное есть десять вертикальных задач и задача с одним словом, которые предстоит решить учащимся. (пример: 452 x 36)
4-6 классы
Почему длина носа не может быть двенадцать дюймов? Чтобы найти ответ на загадку, решите трехзначные задачи на двузначное умножение.
4–6 классы
Умножайте, чтобы найти ответы, и складывайте продукты в кроссворд. (пример: 766 x 11)
4-6 классы
На этой странице есть символы секретного кода, которые учащиеся должны расшифровать. После использования цифрового ключа для выявления факторов учащиеся умножаются, чтобы найти продукты.
4-й и 5-й классы
Решите задачи умножения 3-значного на 2-значное. Затем приклейте кусочки пазла в правильные места на сетке, чтобы увидеть изображение пирата.
с 4-го по 6-й классы
Задачи со словами для тренировки умножения 3-значных чисел на 2-значные числа (пример: 299 x 22)
4-6-й классы
Следуйте инструкциям, чтобы умножить 3-значные числа на 2-значные числа. Например: Найдите произведение чисел в кругах (320 и 30)
с 4-го по 6-й классы
Каждая задача на этом листе имеет трехзначный множитель и двузначный множитель. Студенты переписывают каждую задачу по вертикали и решают.(пример: 193 x 37)
4-й и 5-й классы
Математические упражнения на миллиметровой бумаге; 3 цифры умножить на 2 цифры (пример: 678 x 23)
с 4-го по 6-й классы
Умножение на тему монстра; 3 цифры умножить на 2 цифры (пример: 345 x 82)
С 4-го по 6-й классы
Умножайте 4-значные числа на 2-значные числа. (пример: 2,657 x 28) Затем используйте продукты, чтобы разгадать забавную загадку.
С 4-го по 6-й классы
Решите каждую задачу умножения с 3 на 2 цифры.Показать свою работу. Затем отсканируйте QR-код с помощью iPad или смартфона, чтобы проверить свой ответ.
(Примечание: этот рабочий лист требует, чтобы учащиеся использовали смартфон или планшет со сканером QR-кода.)
4-й и 5-й классы
Отсканируйте QR-код с помощью планшета или смартфона, чтобы отобразить проблему со словами. Решите проблему со словом и покажите свою работу.
(Примечание: этот рабочий лист требует, чтобы учащиеся использовали смартфон или планшет со сканером QR-кода.)
4-й и 5-й классы
Умножение 2- и 3-значных чисел
Урок 2: Умножение 2- и 3-значных чисел
/ ru / multiplicationdivision / от введения к умножению / содержание /
Задачи сложного умножения
Умножая число или сумму, вы на увеличиваете во много раз.Из «Введение в умножение» вы узнали, что умножение может быть способом понять вещи, которые происходят в реальной жизни. Например, представьте, что в магазине продаются коробки с грушами. В маленьких ящиках по груш, по 5 груш. Вы покупаете , две . Вы можете написать такую ситуацию и использовать таблицу умножения на для ее решения:
Теперь представьте, что вы решили купить двух больших коробок по , содержащих 14 груш в каждой. Эта ситуация будет выглядеть так:
Эту проблему решить сложнее.Подсчет груш займет некоторое время. К тому же в таблице умножения нет 14. К счастью, есть способ записать проблему, чтобы можно было разбить ее на более мелкие части. Это называется , укладка . Это означает, что мы будем писать числа друг над другом, , а не рядом.
Давайте попрактикуемся в наложении этой задачи, 14 x 2.
Сначала напишите числа друг над другом. Хорошая привычка всегда писать сверху большее число .Если вы этого не сделаете, решить проблему будет труднее.
Затем напишите знак , умноженный на , напротив левых чисел.
Вместо знака равно поставьте черту под числом внизу.
Обратите внимание, как числа выровнены до справа ?
Когда вы пишете задачу умножения с накоплением, всегда следите за тем, чтобы числа были выстроены таким образом.
Например, давайте рассмотрим другую задачу, 5 x 112.Видите, как 2 находится прямо над 5?
Также обратите внимание, что мы поместили вверху большее число , хотя это было второе число в нашем исходном выражении.
Всегда настраивайте задачи умножения с накоплением одинаково: с большим числом наверху …
Всегда настраивайте задачи умножения с накоплением одинаково: с большим числом наверху … и правильными цифрами выстроились в очередь.
Решение задач сложного умножения
На первый взгляд задачи сложенного умножения могут показаться довольно сложными.Не волнуйтесь! Если вы можете решить проблемы из «Введение в умножение», вы также сможете научиться решать эти проблемы. Чтобы умножать большие числа, вы будете использовать те же базовые навыки, что и для умножения маленьких. Вы даже можете использовать те же инструменты, например, умножить на .
Давайте посмотрим, как работает решение задач умножения с накоплением.
Помните пример с двумя коробками, в каждой по 14 груш? Чтобы узнать, сколько всего груш, решим эту задачу: 14 x 2.
Когда вы умножаете сложенные числа, вы начинаете с правой цифры в нижнем числе задачи. Наше нижнее число состоит только из одной цифры: 2.
Мы умножим 2 на верхнее число, 14. Поскольку в таблице умножения нет 14, нам придется умножать по одной цифре за раз.
Как обычно, решим проблему с справа налево . Итак, мы умножим 2 на цифру в верхнем правом углу . Вот, это 4.
Теперь пришло время решить 2 x 4. Мы можем использовать таблицу умножения.
2 x 4 равно 8. Запишем 8 под 2 и 4.
Теперь умножим 2 на следующую цифру слева: 1.
Теперь решим 2 x 1.
Всякий раз, когда вы умножаете число на 1, это число остается таким же, как . Итак, 2 x 1 равно 2. Чтобы быть уверенным, мы проверим таблицу умножения.
Напишите 2 под линией, прямо под 1.
Готово! Всего у нас 28, или двадцать восемь. 14 x 2 = 28.
Попрактикуемся с другой задачей, 31 x 7.
Всегда начинайте с цифры справа внизу . Здесь это 7.
Сначала умножьте 7 на цифру в верхнем правом углу, 1.
7 x 1 равно 7. Запишите 7 прямо под цифрами, которые мы только что умножили.
Затем мы умножим 7 на следующую цифру слева.Это 3.
Мы будем использовать таблицу умножения для решения 7 x 3.
7 x 3 равно 21. Обязательно выровняйте числа так, чтобы правая цифра 21, 1 была прямой под 3.
Наш ответ — 217. Итак, 31 x 7 = 217.
Попробуйте это!
Сложите и решите эти задачи умножения. Затем проверьте свой ответ, введя его в поле.
Использование переноски
На последней странице вы практиковались в умножении вертикально сложенных чисел.Некоторые проблемы требуют дополнительного шага. Давайте посмотрим на следующую задачу:
Если вы попытаетесь умножить 9 x 5, вы можете заметить, что нет места для записи произведения 45. Когда произведение двух чисел больше 9 , вам нужно будет использовать метод под названием , несущий . Если вы знаете, как складывать большие числа, вы, возможно, помните, как переносили в дополнение. Посмотрим, как это работает при умножении.
Давайте попробуем решить задачу, которую мы только что рассмотрели, 29 x 5.
Как обычно, мы начнем с умножения 5 на верхнюю правую цифру, 9.
Согласно нашей таблице умножения 5 x 9 равно 45, но нет места для записи обеих цифр под 5 и 9.
Правую цифру 5 запишем под чертой …
Под чертой напишем правую цифру 5 … затем перенесем левая цифра, 4, до следующего набора цифр в задаче.
Посмотрите, как это работает? Мы умножили 5 на 9 и получили 45.Мы поместили 5 под линией, перенесли 4 и поместили ее над следующим набором цифр.
Теперь пора сделать следующий шаг. Это то же самое, что и с любой другой задачей умножения. Умножим 5 x 2.
5 x 2 = 10. Впрочем, 10 под чертой пока писать не будем — еще один шаг.
Помните номер, который у нас был, 4?
Нам нужно к добавить к нашему продукту, 10.
4 + 10 равно 14.
Напишем 14 под строкой.
Наше общее количество составляет 145. Теперь мы знаем, что 29 x 5 = 145.
Давайте попробуем другую задачу, просто для практики. 208 x 6.
Сначала мы умножаем нижнее число 6 на цифру в правом верхнем углу. Это 8.
6 x 8 равно 48.
Мы напишем 8 под чертой …
Мы напишем 8 под чертой … и перенесем 4.Поместим его над следующей цифрой.
Следующая цифра — 0.
Все, что умножено на ноль, равно 0, поэтому мы знаем, что 6 x 0 = 0.
Помните, мы еще не пишем 0 под линией. Мы должны добавить его к четырем только что перенесенным.
4 + 0 = 4. Напишем 4 под строкой.
Наконец, мы умножаем 6 и 2.
6 x 2 = 12, поэтому мы напишем 12 под линией.
Готово! Ответ: 1248, или одна тысяча двести сорок восемь.208 x 6 = 1248.
Попробуй!
Сложите и решите эти задачи умножения. Затем проверьте свой ответ, введя его в поле.
Умножение больших чисел
На последних нескольких страницах вы тренировались умножать большие числа на маленькие. Что произойдет, если вам нужно умножить два больших числа?
Например, представьте, что ваш счет за мобильный телефон составляет 43 доллара в месяц . В году 12 месяца, поэтому, чтобы узнать, сколько вы платите за свой телефон каждый год, вы можете решить для 43 x 12.Вы могли бы написать такое выражение:
Сначала эта проблема может показаться сложной, но не беспокойтесь. Если вы можете умножать маленькие числа, вы можете умножать и большие числа. Все, что вам нужно сделать, это разделить эту большую проблему на несколько более мелких. Как всегда, вы можете воспользоваться таблицей умножения .
Чтобы решить такую большую задачу, начните с тех же шагов, которые вы используете для решения любой другой задачи умножения.
Как всегда, вы начинаете с цифры в правом нижнем углу.Здесь это 2.
Мы умножим это на цифру в правом верхнем углу, 3.
Благодаря нашей таблице умножения мы знаем, что 3 x 2 равно 6.
Мы будем напишите 6 под линией в крайнем правом углу.
Затем мы умножим 2 x 4.
2 x 4 равно 8.
Напишите 8 под строкой, прямо под 4.
ОК. Первая половина задачи сделана.
А теперь пора снова взглянуть на нижнюю цифру.
Мы собираемся умножить следующую цифру. Это 1.
Сначала умножьте 1 на верхнее число справа. Здесь это 3.
1 x 3 равно 3 … но мы не собираемся писать 3 в обычном месте.
Вместо того, чтобы записывать 3 справа , как мы обычно делаем …
Вместо того, чтобы записывать 3 справа , как мы обычно делаем … мы собираемся написать он находится на одну позицию слева под вторым набором цифр.
Рекомендуется отметить оставленное вами место пустым. Таким образом, вы будете знать, что нельзя ничего случайно там написать. Мы добавим 0, так как ноль — это то же самое, что ничего .
Теперь давайте умножим последний набор чисел. Это 1 x 4.
1 x 4 = 4. Мы запишем 4 под строкой слева от 3, которые мы только что написали.
Последний шаг. Чтобы получить окончательный ответ, мы должны прибавить к числам, которые мы только что получили в результате умножения.
Как всегда, начнем добавлять справа.
6 + 0 равно 6. Запишем 6 под линией.
Далее, 8 + 3.
8 + 3 равно 11. Поскольку 11 — это двухзначное число, нам придется нести его.
Запишите правую цифру 1 под 8 и 3 …
Запишите левую цифру 1 под 8 и 3 … затем перенесите правую цифру и поместите ее над цифрой, чтобы слева.
Наконец, мы добавим 4 к только что перенесенной единице.
4 + 1 равно 5.
Готово! Наше общее количество составляет 516. Другими словами, 43 x 12 = 516.
Попробуйте это!
Сложите и умножьте эти двузначные числа. Затем проверьте свой ответ, введя его в поле.
Умножение двух трехзначных чисел
Умножение больших чисел всегда работает одинаково, независимо от того, сколько цифр они имеют. При умножении будьте осторожны, записывая числа в правильных местах.Давайте рассмотрим задачу с двумя 3-значными числами , чтобы увидеть, как это работает с еще большими числами.
Давайте попробуем эту задачу: 601 x 243.
Как всегда, начните с умножения правой нижней цифры на верхнюю правую цифру. Итак, 3 x 1.
Благодаря нашей таблице умножения мы знаем, что 3 x 1 равно 3. Запишите 3 под линией, в крайнем правом углу.
Теперь умножьте 3 на следующее число, 0.
Все, что умножено на ноль, равно 0, поэтому напишите 0 под строкой, рядом с 3.
Далее, 3 x 6.
3 x 6 = 18. Напишите 18 под линией.
Мы закончили с первой цифрой в нижнем числе.
Затем умножьте на второе число внизу, 4.
4 x 1 равно 4. Помните, вы не собираетесь писать 4 до упора вправо.
Вместо этого напишите 4 на одну позицию слева под вторым набором чисел.
Чтобы все было выровнено, мы поместим ноль в качестве заполнителя справа от четырех.
Теперь перейдем к следующему числу сверху — 0.
4 x 0 равно 0. Напишите 0 под линией.
Затем умножьте 4 на последнюю цифру в верхнем числе — 6.
4 x 6 равно 24. Напишите 24 под линией.
Мы готовы умножить на последнюю цифру в нашем нижнем числе — 2.
Как всегда, начинайте с верхней правой цифры 1.
2 x 1 равно 2.
Мы запишем 2 под строкой, два пробела справа.
Обратите внимание, куда мы поместили 2.
Когда мы умножили на первую цифру в нижнем числе …
Когда мы умножили на первые цифры в нижнем числе .. .мы выстроили продукт до конца вправо .
Когда мы умножили на вторую цифру …
Когда мы умножили на вторую цифру … мы написали произведение с одним пробелом слева.
Теперь, когда мы умножили на третью цифру …
Теперь, когда мы умножили на третью цифру … мы поместили произведение на два пробелов слева.
Вы могли заметить закономерность.Каждый раз, когда мы умножали новую цифру, мы записывали произведение на одну цифру левее. Это верно независимо от того, сколько цифр в числах, на которые вы умножаете.
Вернемся к нашей проблеме. Мы просто умножили 2 x 1.
Следующая цифра — 0.
2 x 0 — 0. Напишите 0 под линией.
Наконец, умножьте 2 x 6.
2 x 6 равно 12. Напишите 12 под линией.
Пора добавлять.Как всегда, начните с цифр справа. Здесь это означает, что мы складываем 3 + 0 + 0.
3 + 0 + 0 = 3. Напишите 3 прямо под только что добавленными цифрами.
Затем мы добавим 0 + 4 + 0.
0 + 4 + 0 равно 4.
Теперь следующий набор цифр, 8 + 0 + 2.
8 + 0 + 2 = 10. 10 — это двузначное число, поэтому нам нужно нести . Напишите 0 под только что добавленными цифрами и поместите 1 над следующим набором цифр.
Пришло время добавить 1, которую мы только что принесли. Это означает, что мы решаем для 1 + 1+ 4 + 0.
1 + 1 + 4 + 0 = 6. Напишите 6 под линией.
Далее, 2 + 2.
2 + 2 = 4. Напишите 4 под строкой.
Слева всего одна цифра — 1.
Один плюс ничего — 1, поэтому мы напишем 1 под линией.
Наконец-то мы закончили! Всего у нас 146 043 человека, или сто сорок шесть тысяч сорок три.601 х 243 = 146 043.
Какая огромная цифра! Если проблема показалась сложной, не волнуйтесь. Вам редко понадобится умножать такие большие числа. Когда вы это сделаете, вы всегда можете использовать калькулятор. Тем не менее, хорошо знать, как это сделать. Если вы можете умножить эти проблемы, вы можете умножить все, что угодно.
Практика!
Практикуйтесь в умножении больших чисел. Затем проверьте свой ответ, введя его в поле.
Набор 1
Набор 2
Набор 3
/ ru / multiplicationdivision / video-multiplication / content /
Интерактивный урок математики | Умножение 2
Интерактивная математическая практика — умножение двузначных и трехзначных чисел на однозначные числа
Пришло время попрактиковаться в базовых навыках умножения! На этом пятом уроке умножения на уровне класса ученики будут практиковаться в умножении двух- и трехзначных чисел на однозначные числа.Задачи умножения представлены в нескольких форматах: задачи вертикального умножения, задачи горизонтального умножения и задачи умножения слов. Вот несколько примеров математических задач, которые ученики могут задать в этом практическом онлайн-упражнении по математике: «22 x 7 =», «876 x 3 =» и «PTA школы Discovery Charter School проводила социальную встречу с мороженым. Они заказали четыре коробки с мороженым. 480 пластиковых ложек для этого мероприятия. Сколько всего ложек заказала ОТА? »
Если учащимся нужна дополнительная помощь в решении их задач умножения, они могут щелкнуть кнопку «Подсказка» на экране практики.Им будет предложено сделать первый шаг в решении проблемы, умножив единицы. Если учащиеся ответят на вопрос неправильно, им будет показана страница с подробным объяснением с правильным ответом, включая настраиваемую графику с пошаговыми инструкциями по правильному решению задачи умножения, чтобы учащиеся могли учиться на своих ошибках и совершенствоваться. их навыки.
Как работает iKnowIt.com?
Как и все интерактивные практические занятия по математике в разделе «Я знаю», этот базовый урок умножения включает в себя несколько функций, которые помогают учащимся максимально эффективно использовать время на практике.Счетчик прогресса в правом верхнем углу экрана показывает учащимся, сколько математических задач они решили на уроке и сколько осталось выполнить. Счетчик результатов внизу, который показывает им, сколько математических задач они решили правильно до сих пор. Значок динамика в верхнем левом углу экрана дает учащимся возможность прочитать им вопрос вслух и внятным голосом. Этот вариант отлично подходит для студентов ESL / ELL или студентов, которые предпочитают слуховое обучение.
Мы надеемся, что когда вы опробуете этот урок умножения в пятом классе со своим классом, вам и вашим ученикам понравится яркий и красочный дизайн нашей интерактивной учебной программы по математике, включая удобные для детей функции, причудливые анимированные персонажи и мотивирующую систему вознаграждений. .Обязательно изучите сотни других математических тем, доступных на «Я это знаю».
Бесплатная пробная версия и варианты членства
Подпишитесь на бесплатную шестидесятидневную пробную версию iKnowIt.com, чтобы ваш класс мог бесплатно опробовать этот базовый урок умножения! В бесплатном пробном режиме ваши ученики смогут бесплатно играть в любую математическую игру на нашем веб-сайте, но они будут ограничены до двадцати пяти вопросов в день на всех уроках математики «Я знаю». Для неограниченного доступа к сайту вам необходимо стать платным участником.
Вот некоторые из преимуществ, которые вы получите как член iKnowIt.com: вы можете создать список классов и добавить в него своих учеников; вы можете назначить индивидуальные имена пользователей и пароли каждому студенту; вы можете дать разным ученикам разные уроки в зависимости от их индивидуальных потребностей и навыков; вы можете изменить настройки урока в любой момент; и вы можете отслеживать успеваемость учащихся на уроках, включая загрузку, отправку по электронной почте и печать отчетов об успеваемости учащихся.
Мы думаем, что вашим ученикам будет легко и весело использовать студенческий интерфейс iKnowIt.ком! Когда они входят на сайт со своим уникальным именем пользователя и паролем, им будет показана удобная для детей домашняя страница, где они найдут уроки, которые нужно пройти, в разделе «Мои задания». У них также будет возможность изучить другие уроки в своем классе, и, если вы разрешите им, они смогут изучить уроки и в других классах. (Уровни оценок отображаются как «Уровень A» — «Уровень E» в режиме ученика.)
Уровень
Этот урок умножения уровня E может быть идеальным для учеников пятого класса.
Общий базовый стандарт
5.NBT.B.5
Число и операции в базе десяти
Учащиеся смогут выполнять операции с многозначными целыми числами и десятичными дробями с точностью до сотых.
Возможно, вас также заинтересует …
Умножение четырехзначных чисел на однозначные числа (уровень E)
На этом пятом уроке математики на уровне своего класса ученики будут практиковаться в умножении четырехзначных чисел на однозначные числа. Студенты будут решать задачи горизонтального умножения, задачи вертикального умножения и задачи умножения слов.
Умножение двухзначных чисел на двухзначные числа (уровень E)
На этом уроке математики для пятого класса учащиеся будут практиковать умножение. К математическим задачам относятся задачи вертикального умножения, задачи горизонтального умножения и задачи умножения слов.

 Ко времени закуривания второго он нацелил свою снайперскую винтовку. Третий человек, который закурит сигарету, будет застрелен, поскольку у снайпера было достаточно времени для подготовки. Правдиво или нет, суеверие прижилось.
Ко времени закуривания второго он нацелил свою снайперскую винтовку. Третий человек, который закурит сигарету, будет застрелен, поскольку у снайпера было достаточно времени для подготовки. Правдиво или нет, суеверие прижилось.

